Finally, PBR is becoming mainstream... But, it's not easy, especially if you want to stay "correct". Are you sure your pipeline has no errors? Do you know the errors you have? What is your ground truth? Acquired data? Path traced solutions?
I'm planning to share some of my notes on PBR methods and certain findings and thoughts, this is a starter, on Brian Karis' excellent "representative point" area lighting as explained in Siggraph's 2013 PBR course.
I won't say much about it actually, mostly because my own research is not cleared for publication yet. If I were you though, I would also keep an eye on GPU Pro 5, as Michal Drobot's publication might change the state of the art once more (and I'm not really teasing, to say the truth I haven't tried his method yet and compared it, but I think it's "better").
As a good PBR renderer (or any renderer really) should know what kind of errors it's committing, I implemented an area light integrator and used it to verify a few ideas, including Epic's:
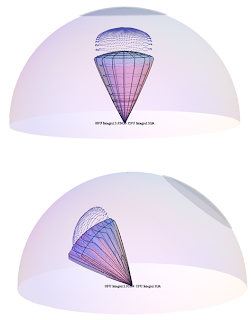 |
| Blue dots: ground truth. Meshed plot: Epic's |
It turns out the representative point solution does not do a great job at "preserving the shape" of the underlying BRDF, and it (quite understandably) just "caps" it with a spherical arc. Also note that at more grazing angles the ground truth is quite different and its cap starts to have a slanted angle as well.
Normalization is also interesting, here I actually thought Epic's method would fare worse (as it seemed to be just an heuristic with not enough justification behind it), but it's actually quite close to ground truth. Always check...
 |
| The smaller, gray mesh is the ground truth, the non-gridded light blue surface is Brian's normalization for the representative point solution, the gridded light blue one is my own version. |
It is possible to do better, with varying degrees of complexity. At a given point things start to be needlessly complicated so, when you start looking at data try not to lose track of what your artists want and what makes a perceivable difference.
Don't do my mistake of staying too long in Mathematica to find a perfect solution, without verifying in actual shaders that you've passed the point where it matters...
Arguably for example, for small lights, the "roughness modification" solution is actually better (don't you love when the old OpenGL fixed-pipeline model, which had a specular power modifier in the lights, is more right than people thought for years?), Brian notes in his writeup that for small lights that is indeed a good method, but you might want to think twice considering if you need big lights or just lights big enough to "correct" for a roughness factor that otherwise would end up wrong in the materials.
 |
| One of my own analytic area approximations |
Some other food for thought:
- How much does hemispherical shadowing (area light dipping under the normal hemisphere visibility) does matter?
- Should more of your sky be represented analytically? Note that it is true that the sun itself has a small arc when seen from the earth, but with the scattering that happens in the sky a larger area could be represented as "area light". The advantages are that it would work better with the BRDF and have more "correct" shadowing...
4 comments:
Great write up! I've been meaning to compare ground truth, my approximation and an analytic integration of a phong lobe expanded with the spherical cap in a blog post but I haven't gotten to it. Looking forward to see what you've come up with on this front.
-Brian
Brian, if you want PM me on twitter and we can chat about the alternatives...
Hi! Would you kindly share the Mathematica code to plot these graphs. Thanks
James: it's a lot of old, messy R&D code, and it's technically property of Activision. Sorry.
Post a Comment