Tonight on Masterchef, we'll try to cook a G-Buffer encoding that is:
- Fast when implemented in a shader
- As compact as possible
- Makes sense under linear interpolation (hardware "blendable", for pixel-shader based decals)
- So we assume no pixel sync custom blending. On a fixed hardware like console's GPUs it would be probably possible to sort decals to not overlap often in screen-space and add waits so read-write of the same buffer never generates data races, but it's not easy.
- As stable as possible, and secondarily as precise as possible.
Normal encodings are a well studied topic, both in computer science and due to their relation with sphere unwrapping and cartographic projections of the globe. Each of the aforementioned objectives, taken singularly, is quite simple to achieve.
Nothing is faster than keeping normals in their natural representations, as a three component vector, and this representation is also the one that makes most sense under linear interpolation (renormalizing afterwards of course).
Unfortunately storing three components means we're wasting a lot of bits, as most bit combinations will yield something that is not a normal vector, so most encodings are unused. In fact we're using just a thin surface of a sphere of valid encodings inside a cubic space of minus one to one components (in 32bit floating point we'll get about 51bits worth of normals out of the 3x32=96bits storage).
If we wanted to go as compact as possible, Crytek's "best fit" normals are one of the best possible representations, together with the octahedral projection (which has a faster encoding and almost the same decoding cost).
Best fit normals aren't the absolute optimal, as they chose the closest representation among the directions contained in the encoding cube space, so they are still constrained to a fixed set of directions, but they are quite great and easy to implement in a shader.
Unfortunately these schemes aren't "blendable" at all. Octahedral normals have discontinuities on half of the normal hemisphere which won't allow blending even if we considered the encoding square to wrap around in a toroidal topology. Best fit normals are all of different lengths, even for very close directions (that's they key for not wasting encode space), so really there is no continuity at all.
Finally, stability. That usually comes from world-space normal encodings, on the account that most games have a varying view more often than they have moving objects with a static view.
Finally, stability. That usually comes from world-space normal encodings, on the account that most games have a varying view more often than they have moving objects with a static view.
World-space two-component encodings can't be hardware "blendable" though, as they will always have a discontinuity on the normal sphere in order to unwrap it.
Object-space and tangent-space encodings are hard because we'll have to store these spaces in the g-buffer, which ends up taking encode space.
View-space can allow blending of two-component encodings by "hiding" the discontinuity in the back-faces of objects so we don't "see" it, but in practice with less than 12 bits per component you end up seeing wobbling on very smooth specular objects as not only normals "snap" into their next representable position as we strafe the camera, but there is also a "fighting" of the precise view-to-world transform we apply during decoding with the quantized normal representation. As we don't have 12bit frame-buffer formats, we'll need to use two 16-bit components, which is not very compact.
So you get quite a puzzle to solve. In the following I'll sketch two possible recipes to try to alleviate these problems.
Object-space and tangent-space encodings are hard because we'll have to store these spaces in the g-buffer, which ends up taking encode space.
View-space can allow blending of two-component encodings by "hiding" the discontinuity in the back-faces of objects so we don't "see" it, but in practice with less than 12 bits per component you end up seeing wobbling on very smooth specular objects as not only normals "snap" into their next representable position as we strafe the camera, but there is also a "fighting" of the precise view-to-world transform we apply during decoding with the quantized normal representation. As we don't have 12bit frame-buffer formats, we'll need to use two 16-bit components, which is not very compact.
So you get quite a puzzle to solve. In the following I'll sketch two possible recipes to try to alleviate these problems.
- Improving view-space projection.
We don't have a twelve bits format. But we do have a 10-10-10-2 format and a 11-11-10 one. The eleven bits floats don't help us much because of their uneven precision distribution (and with no sign bit we can't even center the most precision on the middle of the encoding space), but maybe we can devise some tricks to make ten bits "look like" twelve.
In screen-space, if we were ok never to have perfectly smooth mirrors, we could add some noise to gain one bit (dithering). Another idea could be to "blur" normals while decoding them, looking at their neighbours, but it's slow and it would require some logic to avoid smoothing discontinuities and normal map details, so I didn't even start with that.
A better idea is to look at all the projections and see how they do distribute their precision. Most studies on normal encodings and sphere unwrapping aim to optimize precision over the entire sphere, but here we really don't want that. In fact, we already know we're using view-space exactly to "hide" some of the sphere space, where we'll place the projection discontinuity.
It's common knowledge that we need more than a hemisphere worth of normals for view-space encodings, but how much exactly, and why?
Some of it is due to normal-mapping, that can push normals to face backwards, but that's at least questionable, as these normal-map details should have been hidden by occlusion, where they an actual geometric displacement.
Most of the reason we need to consider more than an hemisphere is due to the perspective projection we do after view-space transform, which makes the view-vector not constant in screen-space. We can see normals around the sides of objects at the edges of the screen that point backwards in view-space.
In order to fight this we can build a view matrix per pixel using the view vector as the z-axis of the space and then encode only an hemisphere (or so) of normals around it. This works, and it really helps eliminating the "wobble" due to the fighting precisions of the encode and view-space matrix, but it's not particularly fast.
- Encode-space tricks.
Working with projections is fun, and I won't stop you from spending days thinking about them and how to make spherical projections work only on parts of the sphere or how to extend hemispherical projections to get a bit more "gutter" space, how to spend more bits on the front-faces and so on. Likely you'll re-derive Lambert's azimuthal equal-area projection a couple of times in the process, by mistake.
What I've found interesting though after all these experiments, is that you can make your life easier by looking at the encode space (the unit square you're projection the normals to) instead, starting with a simple projection (equal-area is a good choice):
- You can simply clip away some normals by "zooming" in the region of the encode space you'll need.
- You can approximate the per-pixel view-space by shifting the encode space so per-pixel the view-vector is its center.
- Furthermore, as your view vector doesn't vary that much, and as your projection doesn't distort these vectors that much, you can approximate the shift by a linear transform of the screen-space 2d coordinate...
- Most projections map normals to a disk, not the entire square (the only two I've found that don't suffer from that are the hemispherical octahedral and the polar space transform/cylindrical projection). You can then map that disk to a square to gain a bit of precision (there are many ways to do so).
- You can take any projection and change its precision distribution if needed by distorting the encode space! Again, many ways to do so, I'd recommend using a piecewise quadratic if you go that route as you'll need to invert whatever function you apply. You can either distort the square by applying a function to each axis, or do the same shifting normals in the disc (easy with the polar transform).
- Note that we can do this not only for normal projections, but also for example to improve the sampling of directions in a cubemap, e.g. for reflections...
 |
| Lambert Equal Area |
 |
| Same encode, with screen-space based "recentering" Note how the encoding on the flat plane isn't constant anymore |
- Encoding using multiple bases.
This recipe comes from chef Alex Fry, from Frostbite's kitchen. It was hinted at by Sebastien Lagarde in his Siggraph presentation but never detailed. This is how I understood it, but really Alex should (and told me he will) provide a detailed explanation (which I'll link here eventually).
When I saw the issues stemming from view-space encodings one of my thoughts was to go world-space. But then you reason a second and realize you can't, because of the inevitable discontinuities.
For a moment I stopped thinking about a projection that double-covers rotations... But then you'll need to store a bit to identify which of the projections you are using (kinda like dual parabolic mapping for example) and that won't be "blendable" either.
We could do some magic if we had wrapping in the blending but we don't, and the blending units aren't going to change anytime soon I believe. So I tossed this away.
And I was wrong. Alex's intuition is that you can indeed use multiple projections and you'll need to store extra bits to encode which projection you used... But, these bits can be read-only during decal-blending!
We can just read which projection was used and project the decal normals in the same space, and live happily ever after! The key is of course to always chose a space that hides your projection discontinuities.
There are many ways to implement this, but to me one very reasonable choice would be to consider the geometric normals when laying down the g-buffer, and chose from a small set of transforms the one with its main axis (the axis we'll orient our normal hemisphere towards during encoding) closest to the surface normal.
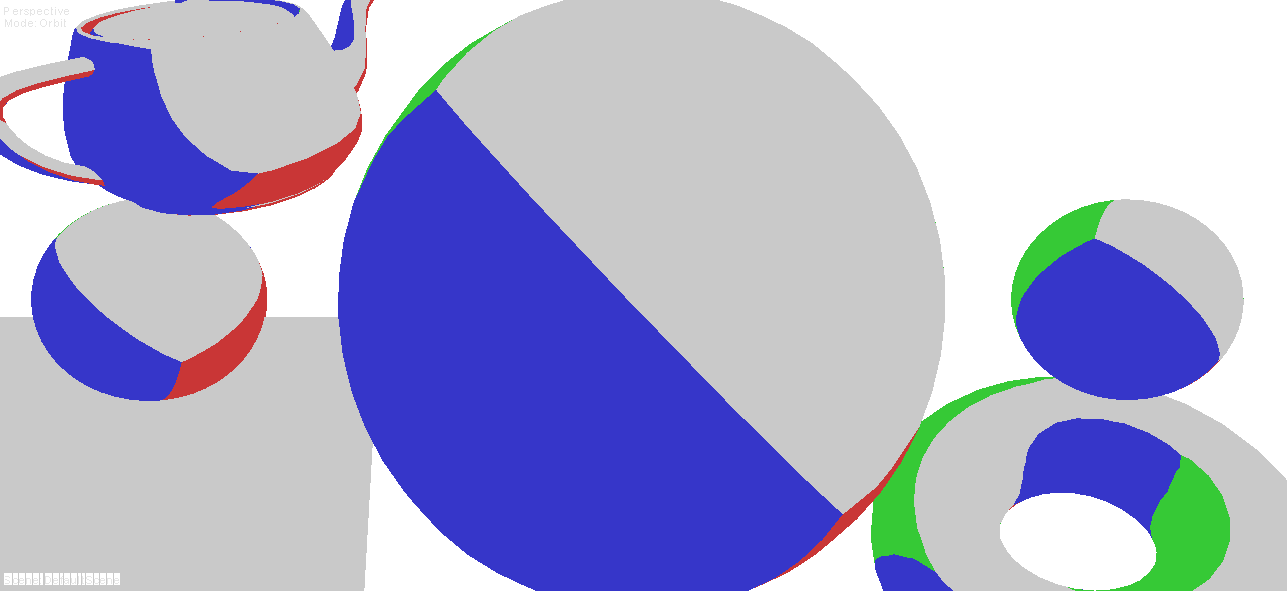 |
| 2-bits tangent spaces |
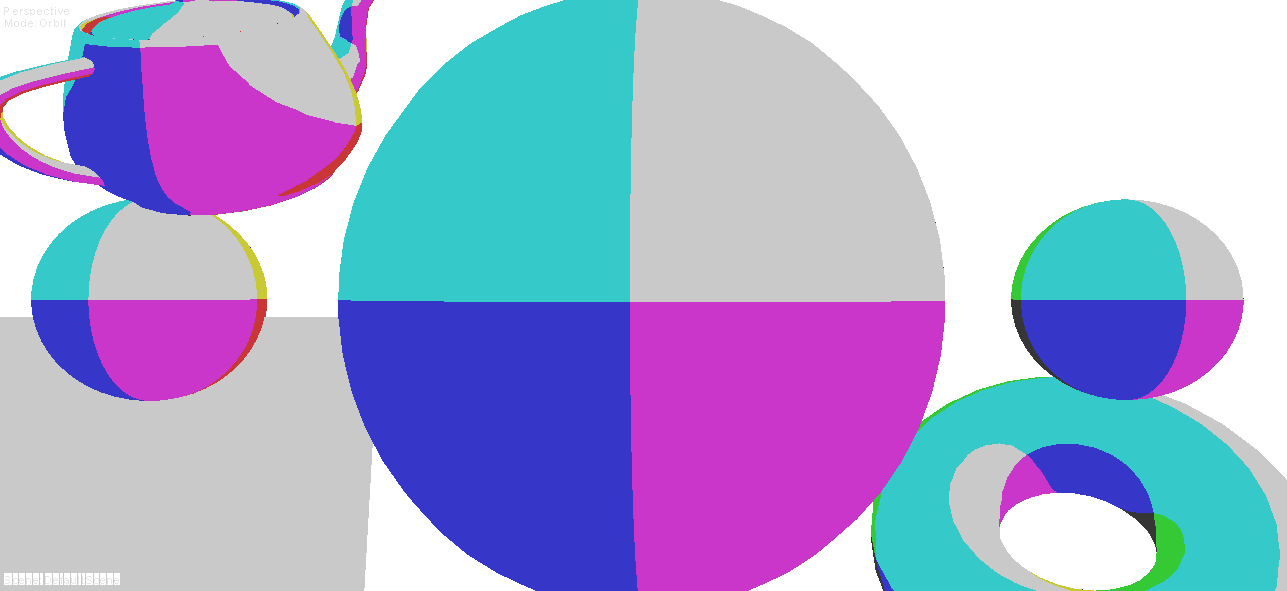 |
| 3-bits tangent spaces |
 |
| 4-bits tangent spaces |
That choice can then be encoded in a few bits that we can stuff anywhere. The two "spare" bits of the 10-10-10-2 format would work, but we can "steal" some bits from any part of the g-buffer (even maintaining the ability to blend that component, by using the most significant bits, reading them in (as we need for the normal encoding anyways) and outputting that component remaining bits (that need to be blended) while keeping the MSB the same across all decals.
I'll probably share some code later, but a good choice would be to use the bases having one axis oriented as the coordinates of the vertices of a signed unitary cube (i.e. spanning minus to plus one), for which the remaining two tangent axes are easy to derive (won't need to re-orthonormalize based on an up vector as it's usually done).
Finally, note how this encode gives us a representation that plays nicely with hardware blending, but it's also more precise than a two-component 10-10 projection if done right. Each encoding space will in fact take care of a subset of the normals on a sphere, namely all the normals closest to its main axis.
Thus, we know that the subsequent normal projection to a two component representation have to take care only of a subset of all possible normals (a hemisphere worth of them, for decals to be able to blend, plus the solid angle of the largest "cell" spanned by the tangent spaces on the sphere), and more spaces (and more bits) we have less normals we'll have to encode for each (e.g. with only one extra bit, the TS would divide the sphere in two halves, and we'll need in each to encode a sphere worth of normals to allow decals to blend, which would be a bad idea).
So, if we engineer the projection to encode only the normals it has to, we can effectively gain precision as we add bits to the space selection.
Conversely beware of encoding more normals than needed, as that can create creases as you move from one space to another on the sphere, when applying normal maps, as certain points will have more "slack" space to encode normals and some others less, you'll have to make sure you won't end up pushing the normals outside the tangent-space hemisphere at any surface point.
- Conclusions & Further references:
Once again we have a pretty fundamental problem in computer graphics that still is a potential source of so much research, and that still is not really solved.
If we look carefully at all our basic primitives, normals, colours, geometry, textures and so on, there is still a lot we don't know or we do badly, often without realizing the problems.
The two encoding strategies I wrote of are certainly a step forward, but still in 10 bits per components you will see quantization patterns on very smooth materials (sharp highlights, mirror-like reflections are the real test case for this). And none of the mappings is optimal, there are still opportunities to stretch and tweak the encoding to use its bits better.
Fun times ahead.
Once again we have a pretty fundamental problem in computer graphics that still is a potential source of so much research, and that still is not really solved.
If we look carefully at all our basic primitives, normals, colours, geometry, textures and so on, there is still a lot we don't know or we do badly, often without realizing the problems.
The two encoding strategies I wrote of are certainly a step forward, but still in 10 bits per components you will see quantization patterns on very smooth materials (sharp highlights, mirror-like reflections are the real test case for this). And none of the mappings is optimal, there are still opportunities to stretch and tweak the encoding to use its bits better.
Fun times ahead.
 |
| A good test case with highly specular materials, flat surfaces, slowly rotating objects/view |
- JCGT's Survey of efficient representations for independent unit vectors is a great resource http://jcgt.org/published/0003/02/01/paper.pdf
- Sampling-efficient spherical images http://research.microsoft.com/en-us/um/people/johnsny/papers/spheremap.pdf
- On floating-point normal vectors http://www.researchgate.net/publication/220506046_On_Floating-Point_Normal_Vectors
- Optimized spherical coordinates http://faculty.cs.tamu.edu/schaefer/research/normalCompression.pdf
- A simply way to make your own projections: http://rgba32.blogspot.ca/2011/02/improved-normal-map-distributions.html
- This shows an interesting projection from hemisphere to disc to hemidisc to square... http://research.microsoft.com/en-us/um/people/johnsny/papers/spheremap_tr.pdf
- Blended azimuthal projection http://archive.bridgesmathart.org/2014/bridges2014-103.pdf
- Fast SIMD equal-area mapping http://fileadmin.cs.lth.se/graphics/research/papers/2008/simdmapping/clarberg_simdmapping08_preprint.pdf
- Healpix is cute but slow/wastes some space - http://en.wikipedia.org/wiki/HEALPix
- Flattened octahedron mapping http://www.cs.utah.edu/~emilp/papers/SphereParam.pdf
- Pierce quincuncial (distorted octahedron) http://arxiv.org/ftp/arxiv/papers/1011/1011.3189.pdf
- Another tangentially related paper http://research.microsoft.com/en-us/um/people/hoppe/metricaware.pdf
4 comments:
>"We can just read which projection was used and project the decal normals in the same space,"
yes you get it. In practice this mean you decal can't modify your normal more than the angle authorized by your basis. In our case we use a cube, mean normal can't deviate more than 45° from current cube face axis but in practice it looks ok.
Sebastien: Thanks for reading this.
I suspect using the geometric normal for the basis selection would yield the best results (at least, I think that's the case), dunno if you're doing that or using the base-layer normalmapped normal.
Also I think you can get a bit more precision if you encode the normal in a way that bounds the normals representable in a given basis selection.
The basis choice will span a given solid angle, and you don't need to encode more than an hemisphere+that solid angle. I don't think that normals facing outside the surface tangent hemisphere make much sense...
But if you do so one has to be careful to exactly clamp normals to the surface tangent hemisphere (I guess for regular normalmapping and linear blends that's always the case, but things can go bad with other procedural modifications) otherwise there could be seams due to the fact that some points have more "wiggle" room than others.
I wonder if you guys do restring the normals in such way to gain precision or just use stuff like lambert equal area on the full normal sphere.
Just gonna add some notes here incase anyone else is trying this.
I have implemented this, works pretty well using 10, 10 for UV and 3 bits for the space.
It appears to lose about as much data as encoding with RGB10.
Implemented using 8 spaces (3 bits) to work out the encoding space.
int coordSpace = (int)dot(saturate(IN.vertex.normal > 0), float3(1, 2, 4));
I am using the lamber azimuthal equal area projection as described in this post.
I have however found that using the decoded normal for a reflected vector becomes quite lossy with noticable artifacts on shiny surfaces.
To fixed this i tried adding a blue noise jitter post decode, but the artifacts were still clearly visible.
I tried adding a blue noise jitter to the UV component before it gets quantized instead.
Since i use TAA this worked really well, no artifacts noticable (other than the noise of course)
Bluenoise source - http://momentsingraphics.de/BlueNoise.html
I can't remember anymore the details of my implementation, as it was a while ago (Call of Duty - Black Ops 3) and I tried a ton of different things. I am sure I managed to tweak the view-space projection so that it was shippable, but in the end the world-space with multiple encodings one was the one that shipped.
FWIW I think thought that I ended up using only 2 bits. Not 100% sure though, I think it was 2 bits and carefully made sure the encodings on the different tangent frames did not overlap too much. Some overlap is needed of course otherwise decal blending risks to "slam" on the boundary of the permitted space, but especially when selecting the encoding space using the geometric normal (and not the normal-mapped one) you don't need too much slack.
In theory you need each space to cover only a hemisphere plus the angular extent that the quadrant of that tangent space covers, so you can ensure that in the worst case, when discretizing the geometric normal to the chosen tangent space, you still have space around it to encode the full hemisphere around the original surface.
Post a Comment