How to render it. Ten ideas to solve Computer Graphics problems.

Pre-Ramble.

A decade ago or so, yours truly was a greener but enthusiastic computer engineer, working in production to make videogames look prettier. At a point, I had, in my naivety, an idea for a book about the field, and went* to a great mentor, with it.

* messaged over I think MSN messenger. Could have been Skype, could have been ICQ, but I think it was MSN...

He warned me about the amount of toiling required to write a book, and the meager rewards, so that, coupled with my inherent laziness, was the end of it.

The mentor was a guy called Christer Ericson, who I had the fortune of working for later in life, and among many achievements, is the author of Real-time Collision Detection, still to this date, one of the best technical books I’ve read on any subject.

The idea was to make a book not about specific solutions and technologies, but about conceptual tools that seemed to me at the time to be recurringly useful in my field (game engine development).

He was right then, and I am definitely no less lazy now, so, you won’t get a book, but I thought, having accumulated a bit more experience, it might be interesting to meditate on what I’ve found in my career to be useful when it comes to innovation in real-time rendering.

As we'll be talking about tools for innovation, the following is written assuming the reader has enough familiarity with the field - as such, it's perhaps a bit niche. I'd love if others were to write similar posts about other industries though - we have plenty of tools to generate ideas in creative fields, but I've seen fewer around (computer) science.

The metatechniques.

In no specific order, I’ll try to describe ten meta-ideas, tools for thought if you wish, and provide some notable examples of their application.

1. Use the right space.
2. Data representation and its properties.
• Consider the three main phases of computation.
• Consider the dual problem.
3. Compute over time.
4. Think about the limitations of available data.
1. Machine learning as an upper limit.
5. The hierarchy of ground truths.
6. Use computers to help along the way.
7. Humans over math.
8. Find good priors.
9. Delve deep.
10. Shortcut via proxies.

A good way to use these when solving a problem is to map out a design space, try to sketch solutions using a combination of different choices in each axis, and really try to imagine if it would work (i.e. on pen and paper, not going deep into implementation).

Then, from this catalog of possibilities, select a few that are worth refining with some quick experiments, and so on and so forth, keep narrowing down while going deeper.

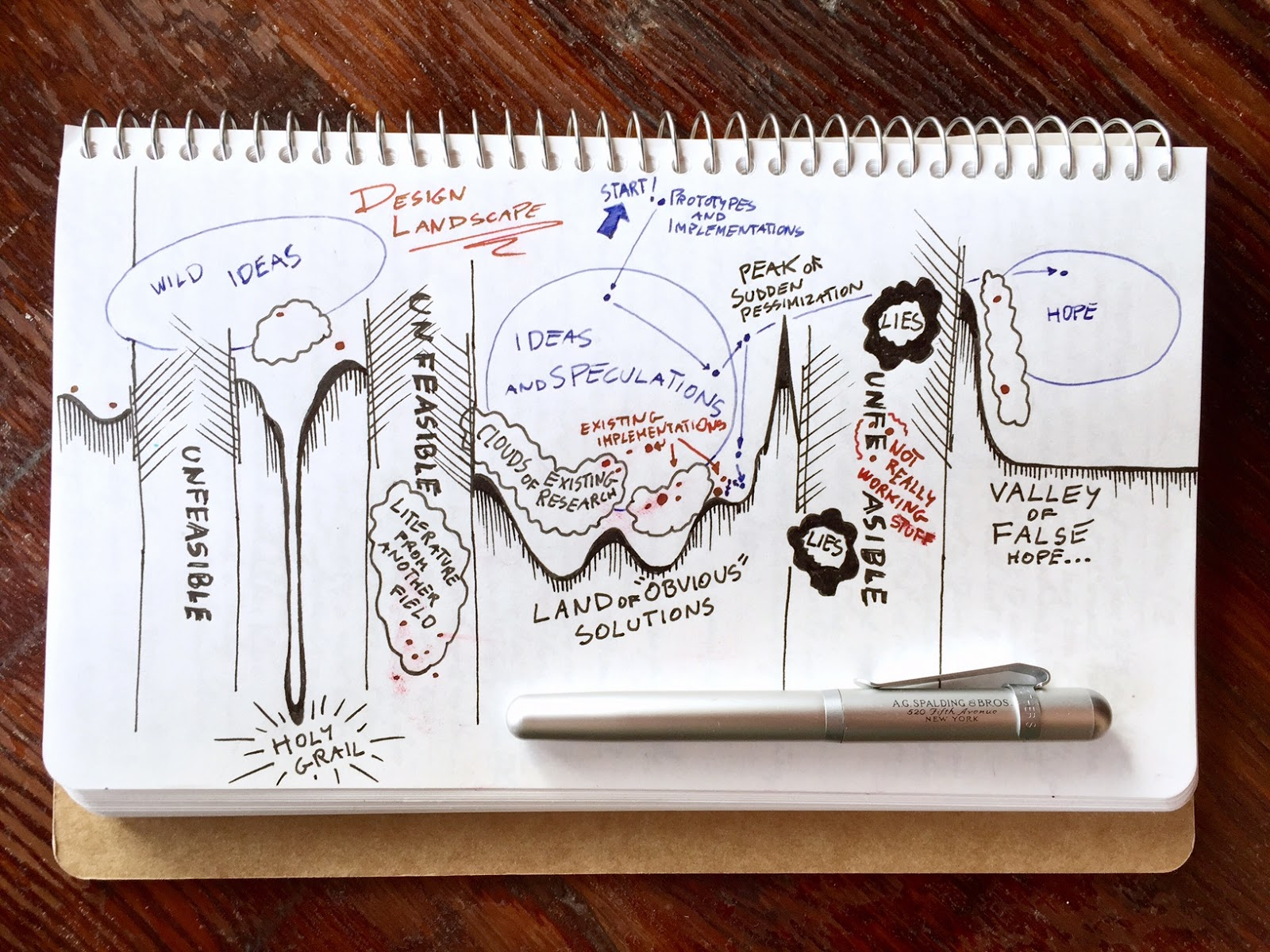Related post: Design optimization landscape

1) Use the right space.

Computer graphics problems can literally be solved from different perspectives, and each offers, typically, different tradeoffs.

Should I work in screen-space? Then I might have an easier time decoupling from scene complexity, and I will most likely work only on what’s visible, but that’s also the main downside (e.g. having to handle disocclusions and not being able to know what’s not in view). Should I work in world-space? In object-space? In “texture”-space, i.e. over a parametrization of the surfaces?

Examples:

• Obviously, SSAO, which really opened the floodgates of screen-space techniques
• Realistic human face rendering for "The Matrix Reloaded"

2) Data representation and its properties.

This is a fundamental principle of computer science; different data structures have fundamentally different properties in terms of which operations they allow to be performed efficiently.

And even if that’s such an obvious point, do you think systematically about it when exploring a problem in real-time rendering?

List all the options and the relative properties. We might be working on signals on a hemisphere, what do we use? Spherical Harmonics? Spherical Gaussians? LTCs? A hemicube? Or we could map from the hemisphere to a circle, and from a circle to a square, to derive a two-dimensional parametrization, and so on.

Voxels or froxels? Vertices or textures? Meshes or point clouds? For any given problem, you can list probably at least a handful of fundamentally different data structures worth investigating.

2B) Consider the three main phases of computation.

Typically, real-time rendering computation is divided into three: scene encoding, solver, and real-time retrieval. Ideally, we use the same data structure for all three, but it might be perfectly fine to consider different encodings for each.

For example, let’s consider global illumination. We could voxelize the scene, then scatter light by walking the voxel data structure, say, employing voxel cone tracing, and finally utilize the data during rendering by directly sampling the voxels. We can even do everything in the same space, using world-space would be the most obvious choice, starting from using a compute 3D voxelizer over the scene. That would be fine. 

But nobody prohibits us to use different data structures in each step, and the end results might be faster. For example, we might want to take our screen-space depth and lift that to a world-space voxel data structure. We could (just spitballing here, not to mean it’s a good idea) generate probes with a voxel render, to approximate scattering. And finally, we could avoid sampling probes in real-time, by say, incrementally generating lightmaps (again, don’t take this as a serious idea).

Imperfect Shadow Maps are a neat example of thinking outside the box in terms of spaces and data structure to solve a problem...

2C) Consider the dual problem.

This is a special case of "the right data" and "the right space" - but it is common enough, and easy to overlook, so it gets a special mention.

All problems have "duals", some in a very mathematical sense, others in a looser interpretation of the world. Often time, looking at these duals yields superior solutions, either because the dual is easier/better to solve, or because one can solve both, exploiting the strengths of each system

A simple example of rigorous duality is in the classic marching cubes algorithm, compared to the surface nets which operates on the dual grid of MC: surface nets are much easier and higher quality!

A more interesting, more philosophical dual, is in the relationship between cells and portals for visibility "versus" occluders and bounding volumes. Think about it :)

3) Compute over time.

This is a simple universal strategy to convert computationally hard problems into something amenable to real-time. Just don’t try to solve anything in a single frame, if it can be done over time, it probably should.

Incremental computation is powerful in many different ways. It exploits the fact that typically, a small percentage of the total data we have to deal with is in the working set.

This is powerful because it is a universal truth of computing, not strictly a rendering idea (think about memory hierarchies, caches, and the cost of moving data around).

Furthermore, it’s perceptually sound. Motion grabs our attention, and our vision system deals with deltas and gradients. So, we can get by with a less perfect solution if it is “hidden” by a bigger change.

Lastly, it is efficient computationally, because we deal with a very strict frame budget (we want to avoid jitter in the framerate) but an uneven computational load (not all frames take the same time). Incremental computation allows us to “fill” gaps in frames that are faster to compute, while still allowing us to end in time if a frame is more complex, by only adding lag to the given incremental algorithm. Thus, we can always utilize our computational resources fully.

Obviously, TAA, but examples here are too numerous to give, it’s probably simpler to note how modern engines look like an abstract mess if one forces all the incremental algorithms to not re-use temporal information. It’s everywhere. 

Parts of Cyberpunk 2077's specular lighting, without temporal 

It’s worth noting also that here I’m not just thinking of temporal reprojection, but all techniques that cache data over time, that update data over multiple frames, and that effectively result in different aspects of the rendering of a frame to operate at entirely decoupled frequencies.

Take modern shadowmaps. Cascades are linked to the view-space frustum, but we might divide them into tiles and cache over frames. Many games then throttle sun movements to happen mostly during camera motion, to hide recomputation artifacts. We might update far cascades at different frequencies than close ones and entirely bail out of updating tiles if we’re over a given frame budget. Finally, we might do shadowmap filtering using stochastic algorithms that are amortized among frames using reprojection.

4) Think about the limitations of available data.

We made some choices, in the previous steps, now it’s time to forecast what results we could get.

This is important in both directions, sometimes we underestimate what’s possible with the data that we can realistically compute in a real-time setting, other times we can “prove” that fundamentally we don’t have enough/the right data, and we need a perspective change.

A good tool to think about this is to try a brute-force solution over our data structures, even if it wouldn’t be feasible in real-time, it would provide a sort of ground truth (more on this later): what’s the absolute best we could do with the data we have.

Some examples, from my personal experience.

• When Crysis came out I was working at a company called Milestone, and I remember Riccardo Minervino, one of our technical artists, dumping the textures in the game, from which we “discovered” something that looked like AO, but looked like it was done in screen-space. What sorcery was that, we were puzzled and amazed. It took though less than a day, unconsciously following some of the lines of thought I’m writing about now, for me to guess that it must have been done with the depth buffer, and from there, that one could try to “simply” raytrace the depth buffer, taking inspiration from relief mapping.
• This ended up not being the actual technique used by Crytek (raymarching is way too slow), but it was even back in the day an example of “best that can be done with the data available” - and when Jorge and I were working on GTAO, one thing that we had as a reference was a raymarched AO that Jorge wrote using only the depth data.
• Similarly, I’ve used this technique a lot when thinking of other screen-space techniques, because these have obvious limitations in terms of available data. Depth-of-field and motion-blur are an example, where even if I never wrote an actual brute-force-with-limited-information solution, I keep that in the back of my mind. I know that the “best” solution would be to scatter (e.g. the DOF particles approach, first seen in Lost Planet, which FWIW on compute nowadays could be more sane), I know that’s too slow (at least, it was when I was doing these things) and that I had to “gather” instead, but to understand the correctness of the gather, you can think of what you’re missing (if anything) comparing to the more correct, but slower, solution.

4B) Machine learning as an upper limit.

The only caveat here is that in many cases the true “best possible” solution goes beyond algorithmic brute force, and instead couples that with some inference. I.e. we don’t have the data we’d like, but can we “guess”? That guessing is the realm of heuristics. 

Lately, the ubiquity of ML opened up an interesting option: to use machine learning as a proxy to validate the “goodness” of data.

For example, in SSAO a typical artifact we get is dark silhouettes around characters, as depth discontinuities are equivalent to long “walls” when interpreting the depth buffer naively (i.e. as a heightfield). But we know that’s bad, and any competent SSAO (or SSR, etc) employs some heuristic to assign some “thickness” to the data in the depth buffer (at least, virtually) to allow rays to pass behind certain objects. That heuristic is a guessing game, how do we know how well we could do? There, training a ML model with ground truth, raytraced AO, and feeding it only the depth-buffer as inputs, can give us an idea of the best we could ever do, even if we are not going to deploy the ML model in real-time, at all.

See also: Deep G-Buffers for GI but remember, here I'm specifically talking about ML as proof of feasibility, not as the final technique to deploy.

5) The hierarchy of ground truths.

The beauty of rendering is that we can pretty much express all our problems in a single equation, we all know it, Kajiya’s Rendering Equation.

From there on, everything is really about making the solution practical, that’s all there is to our job. But we should never forget that the “impractical” solution is great for reference, to understand where our errors are, and to bound the limits of what can be done.

But what is the “true” ground truth? In practice, we should think of a hierarchy. 

At the top, well, there is reality itself, that we can probe with cameras and other means of acquisition. Then, we start layering assumptions and models, even the almighty Rendering Equation already makes many, e.g. we operate under the model of geometrical optics, which has its own assumptions, and even there we don’t take the “full” model, we typically narrow it further down: we discard spectral dependencies, we simplify scattering models and so on.

At the very least, we typically have four levels. First, it’s reality.

Second, is the outermost theoretical model, this is a problem-independent one we just assume for rendering in general, i.e. the flavor of rendering equation, scene representation, material modeling, color spaces, etc we work in.

Then, there is often a further model that we assume true for the specific problem at hand, say, we are Ambient Occlusion, that entire notion of AO being “a thing” is its own simplification of the rendering equation, and certain quality issues stem simply from having made that assumption.

Lastly, there is all that we talked about in the previous point, namely, a further assumption that we can only work with a given subset of data.

Often innovation comes by noticing that some of the assumptions we made along the way were wrong, we simply were ignoring parts of reality that we should not have, that make a perceptual difference. 

What good is it to find a super accurate solution to say, the integral of spherical diffuse lights with Phong shading, if these lights and that shading never exist in the real world? It’s sobering to look back at how often we made these mistakes (and our artists complained that they could not work well with the provided math, and needed more controls, only for us to notice that fundamentally, the model was wrong - point lights anybody?)

Other times, the ground truth is useful only to understand our mistakes, to validate our code, or as a basis for prototyping.

6) Use computers to help along the way.

No, I’m not talking about ChatGPT here.

Numerical optimization, dimensionality reduction, data visualization - in general, we can couple analytic techniques with data exploration, sometimes with surprising results.

The first, more obvious observation, is that in general, we know our problems are not solvable in closed form, we know this directly from the rendering equation, this is all theory that should be so ingrained I won’t repeat it, our integral is recursive, its form even has a name, we know we can’t solve it, we know we can employ numerical techniques and blah blah blah path tracing.

This is not very interesting per se, as we never directly deal with Kajiya’s in real-time, we layer assumptions that make our problem simpler, and we divide it into a myriad of sub-problems, and many of these do indeed have closed-form solutions.

But even in these cases, we might want to further approximate, for performance. Or we might notice that an approximate solution (as in function approximation or look-up tables) with a better model is superior to an exact solution with a more stringent one.

But there is a second layer where computers help, which is to inform our exploration of the problem domain. Working with data, and interacting with it, aids discovery. 

We might visualize a signal and notice it resembles a known function (or that by applying a given transform we improve the visualization) - leading to deductions about the nature of the problem, sometimes that we can reconduct directly to analytic or geometric insights. We might observe that certain variables are not strongly correlated with a given outcome, again, allowing us to understand what matters. Or we might do dimensionality reduction, clustering, and understand that there might be different sub-problems that are worth separating.

To the extreme, we can employ symbolic regression, to try to use brute force computer exploration and have it "tell us" directly what it found. 

Examples. This is more about methodology, and I can't know how much other researchers leverage the same methods, but in the years I've written multiple times about these themes:

• This Siggraph talk
• Data visualization 101

• Some horrible old tools I wrote to connect live programs to data vis

7) Humans over math.

One of the biggest sins of computer engineering in general is not thinking about people, processes, and products. It's the reason why tech fails, companies fail, and careers "fail"... and it definitely extends to research as well, especially if you want to see it applied.

In computer graphics, this manifests in two main issues. First, there is the simple case of forgetting about perceptual error measures. This is a capital sin both in papers (technique X is better by Y by this % MSE) and data-driven results (visualization, approximation...). 

The most obvious issue is to just use mean squared error (a.k.a. L2) everywhere, but often times things can be a bit trickier, as we might seek to improve a specific element in a processing chain that delivers pixels to our faces, and we too often just measure errors in that element alone, discounting the rest of the pipeline which would induce obvious nonlinearities.

In these cases, sometimes we can just measure the error at the end of the pipeline (e.g. on test scenes), and other times we can approximate/mock the parts we don't explicitly consider.

As an example, if we are approximating a given integral of a luminaire with a set BRDF model, we should probably consider that the results would go through a tone mapper, and if we don't want to use a specific one (which might not be wise, especially because that would probably depend on the exposure), we can at least account for the roughly logarithmic nature of human vision...

Note that a variant of this issue is to use the wrong dataset when computing errors or optimizing, for example, one might test a new GPU texture compression method over natural image datasets, while the important use case might be source textures, that have significantly different statistics. All these are subtle mistakes that can cause large errors (and thus, also, the ability to innovate by fixing them...)

The second category of sins is to forget whose life we are trying to improve - namely, the artist's and the end user's. Is a piece of better math useful at all, if nobody can see it? Are you overthinking PBR, or focusing on the wrong parts of the imagining pipeline? What matters for image quality? 

In most cases, the answer would be "the ability of artists to iterate" - and that is something very specific to a given product and production pipeline. 

If you can spend more time with artists, as a computer graphics engineer, you should. 

Nowadays unfortunately productions are so large that this tight collaboration is often unfeasible, artists dwarf engineers by orders of magnitude, and thus we often create some tools with few data points, release them "in the wild" of a production process, where they might or might not be used in the ways they were "supposed" to. Even the misuse is very informative. 

We should always remember that artists have the best eyes, they are our connection to the end users, to the product, and the ones we should trust. If they see something wrong, it probably is. It is our job to figure out why, where, and how to fix it, all these dimensions are part of the researcher's job, but the hint at what is wrong, comes first from art. 

An anecdote I often refer to, because I lived through these days, is when artists had only point lights, and some demanded that lights carried modifiers to the roughness of surfaces they hit. I think this might have even been in the OpenGL fixed function lighting model, but don't quote me there. Well, most of us laughed (and might laugh today, if not paying attention) at the silliness of the request. Only to be humbled by the invention of "roughness modification" as an approximation to area lights...

Here is where I should also mention the idea of taking inspiration from other fields, this is true in general and almost to the same level as suggestions like "take a walk to find solutions" or "talk to other people about the problem you're trying to solve" - i.e. good advice that I didn't feel was specific enough. We know that creativity is the recombination of ideas, and that being a good mix of "deep/vertical" and "wide/horizontal" is important... in life. 

But specifically, here I want to mention the importance of looking at our immediate neighbors: know about art, its tools and language, know about offline rendering, movies, and visual effects, as they can often "predict" where we will go, or as we can re-use their old techniques, look at acquisition and scanning techniques, to understand the deeper nature of certain objects, look at photography and movie making. 

When we think about inspiration, we sometimes limit ourselves to related fields in computer science, but a lot of it comes from entirely different professions, again, humans.

See also:

• Seeing the whole PBR picture and parts of this talk at Intel
• My notes on the rendering research in Fight Night Champion
• Naty's "outside the echo chamber" talk
• Looking at the lighting of a movie set it instructive, I often reference Gregory Crewdson (who uses similar techniques in photography)
• "Kids these days" might think that AO has always been a real-time idea, but it actually comes from movies - including bent normals, in fact, the first time I personally coded bent normals, was because of Landis paper.

8) Find good priors.

A fancy term for assumptions, but here I am specifically thinking of statistics over the inputs of a given problem, not simplifying assumptions over the physics involved. It is often the case in computer graphics that we cannot solve a given problem in general, literally, it is theoretically not solvable. But it can become even easy to solve once we notice that not all inputs are equally likely to be present in natural scenes.

This is the key assumption in most image processing problems, upsampling, denoising, inpainting, de-blurring, and so on. In general, images are made of pixels, and any configuration of pixels is an image. But out of this gigantic space (width x height x color channels = dimensions), only a small set comprises images that make any sense at all, most of the space is occupied, literally, by random crap.

If we have some assumption over what configurations of pixels are more likely, then we can solve problems. For example, in general upsampling has no solution, downsampling is a lossy process, and there is no reason for us to prefer a given upsampled version to another where both would generate the same downsampled results... until we assume a prior. By hand and logic, we can prioritize edges in an image, or gradients, and from there we get all the edge-aware upsampling algorithms we know (or might google). If we can assume more, say, that the images are about faces or text and so on, we can create truly miraculous (hallucination) techniques.

As an aside, specifically for images, this is why deep learning is so powerful - we know that there is a tiny subspace of all possible random pixels that are part of naturally occurring images, but we have a hard time expressing that space by handcrafted rules. So, machine learning comes to the rescue.

This idea though applies to many other domains, not just images. Convolutions are everywhere, sparse signals are everywhere, and noise is everywhere, all these domains can benefit from adopting priors. 

E.g. we might know about radiance in parts of the scene only through some diffuse irradiance probes (e.g. spherical harmonics). Can we hallucinate something for specular lighting? In general, no, in practice, probably. We might assume that lighting is likely to come from a compact set of directions (a single dominant luminaire). Often times is even powerful to assume that lighting comes mostly from the top down, in most natural scenes - e.g. bias AO towards the ground...

See also: an old rant on super-resolution ignorance

9) Delve deep.

This is time-consuming and can be annoying, but it is also one of the reasons why it's a powerful technique. Keep asking "why". Most of what we do, and I feel this applies outside computer graphics as well, is habit or worse, hype. And it makes sense for this to be the case, we simply do not have the time to question every choice, check every assumption, and find all the sources when our products and problems keep growing in complexity.

But for a researcher, it is also a land of opportunity. Often times we can even today, pick a topic at random, a piece of our pipeline, and by simply keep questioning it we'll find fundamental flaws that when corrected yield considerable benefits. 

This is either because of mistakes (they happen), because of changes in assumptions (i.e. what was true in the sixties when a given piece of math was made, is not true today), because we ignored the assumptions (i.e. the original authors knew a given thing was applicable only in a specific context, but we forgot about it), or because we plugged in a given piece of math/algorithm/technology and added large errors while doing it.

A simple example: most integrals of lighting and BRDFs with normalmaps, which cause the hemisphere of incoming light directions to partially be occluded by the surface geometry. We clearly have to take that horizon occlusion into consideration, but we often do not, or if we do it's through quick hacks that were never validated. Or how we use Cook-Torrance-based BRDFs, without remembering that they are valid only up to a given surface smoothness. Or how nobody really knows what to do with colors (What's the right space for lighting? For albedos? To do computation? We put sRGB primaries over everything and call it a day...). But again, this is everywhere, if one has the patience of delving...

10) Shortcut via proxies.

Lastly, this one is a bit different than all the others, in a way a bit more "meta". It is not a technique to find ideas, but one to accelerate the development process of ideas, and it is about creating mockups and prototypes as often as possible, as cheaply as possible.

We should always think - can I mock this up quickly using some shortcut? Especially where it matters, that's to say, around unknowns and uncertain areas. Can I use an offline path tracer, and create a scene that proves what my intuition is telling me? Perhaps for that specific phenomenon, the most important thing is, I don't know, the accuracy of the specular reflection, or the influence of subsurface scattering, or modeling lights a given way...

Can I prove my ideas in two dimensions? Can I use some other engine that is more amenable to live coding and experimentation? Can I modify a plug-in? Can I create a static scene that previews the performance implication of something that I know will need to generate dynamically - say a terrain system or a vegetation system.

Can I do something with pen and paper? Can I build a physical model? Can I gather data from other games, from photos, from acquiring real-world data... Can I leverage tech artists to create mocks? Can I create artificial loads to investigate the performance, on hardware, of certain choices?

Any way you have to write less code, take less time, and answer a question that allows you to explore the solution space faster, is absolutely a priority when it comes to innovation. Our design space is huge! It's unwise to put prematurely all the chips on a given solution, but it is equally unwise to spend too long exploring wide, so the efficiency of the exploration is paramount, in practice.

- Ending rant.

I hope you enjoyed this. In some ways I realize it's a retrospective that I write now as I've, if not closed, at least paused the part of my career that was mostly about graphics research, to learn about other areas that I have not seen before.

It's almost like these youtube ads where people peddle free pamphlets on ten easy steps to become rich with Amazon etc, minus the scam (trust me...). Knowledge sharing is the best pyramid scheme! The more other people innovate, the more I can (have the people who actually write code these days) copy and paste solutions :)

I also like to note how this list could be called "anti-design patterns" (not anti-patterns, which are still patterns), the opposite of DPs in the sense that I hope for these to be starting points for ideas generation, to apply your minds in a creative process, while DPs (ala GoF) are prescribed (terrible) "solutions" meant to be blindly applied. 

I probably should not even mention them because at least in my industry, they are finally effectively dead, after a phase of hype (unfortunately, we are often too mindless in general) - but hey, if I can have one last stab... why not :)